Measurements with autocollimator
Autocollimators are a combination of collimator and telescope sharing the same optical path via a beam splitter. Via the collimator functionality, the structure engraved on the reticle is imaged typically to infinity. The device under test is placed in the optical path and reflects the light back into the autocollimator. This reflected light can be inspected via the telescope functionality.
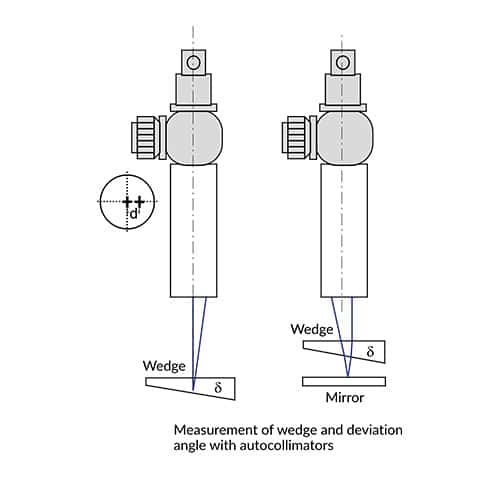
A typical application is the measurement of the tilt angle of the surface that reflects the light back into the autocollimator.
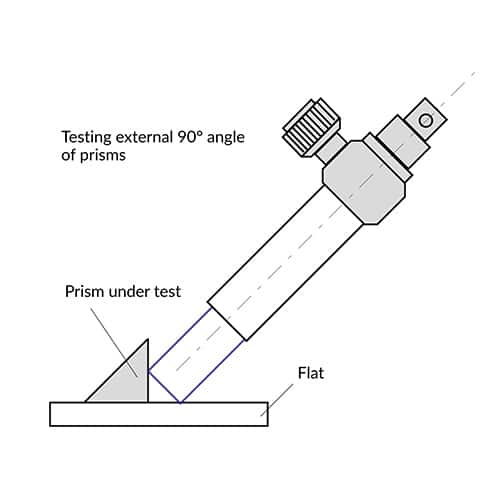
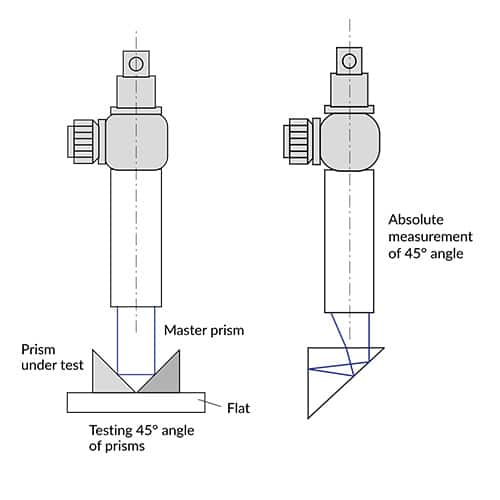
Angle measurement of optical components
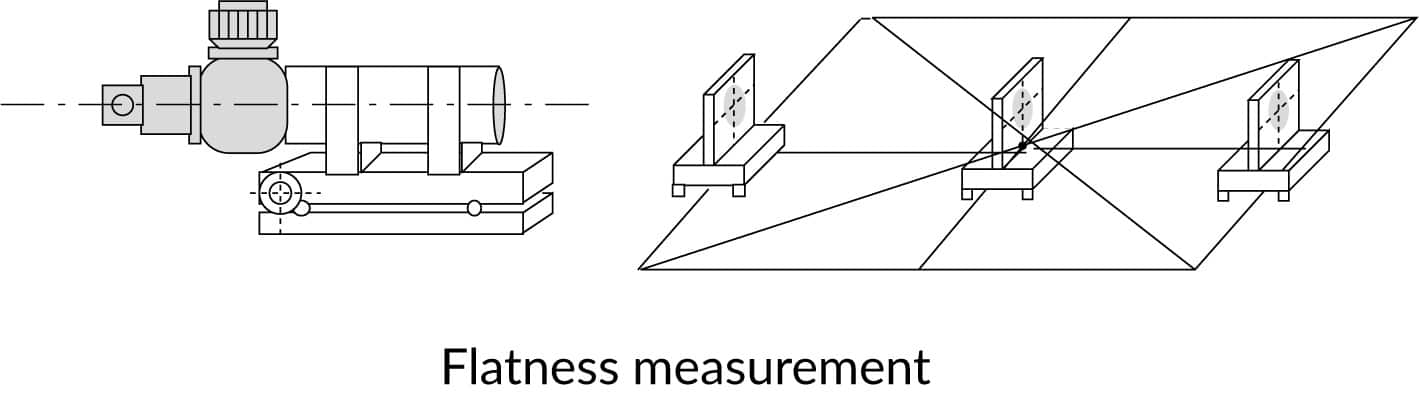
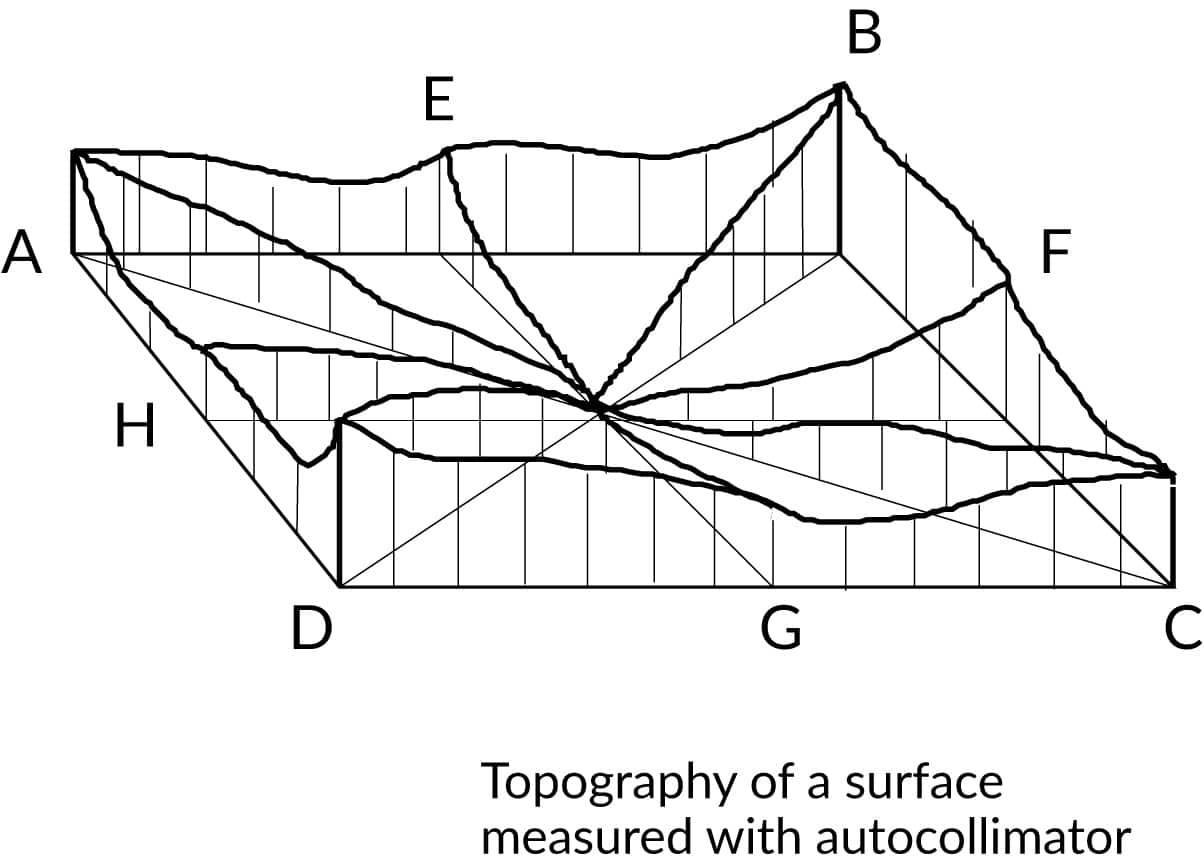
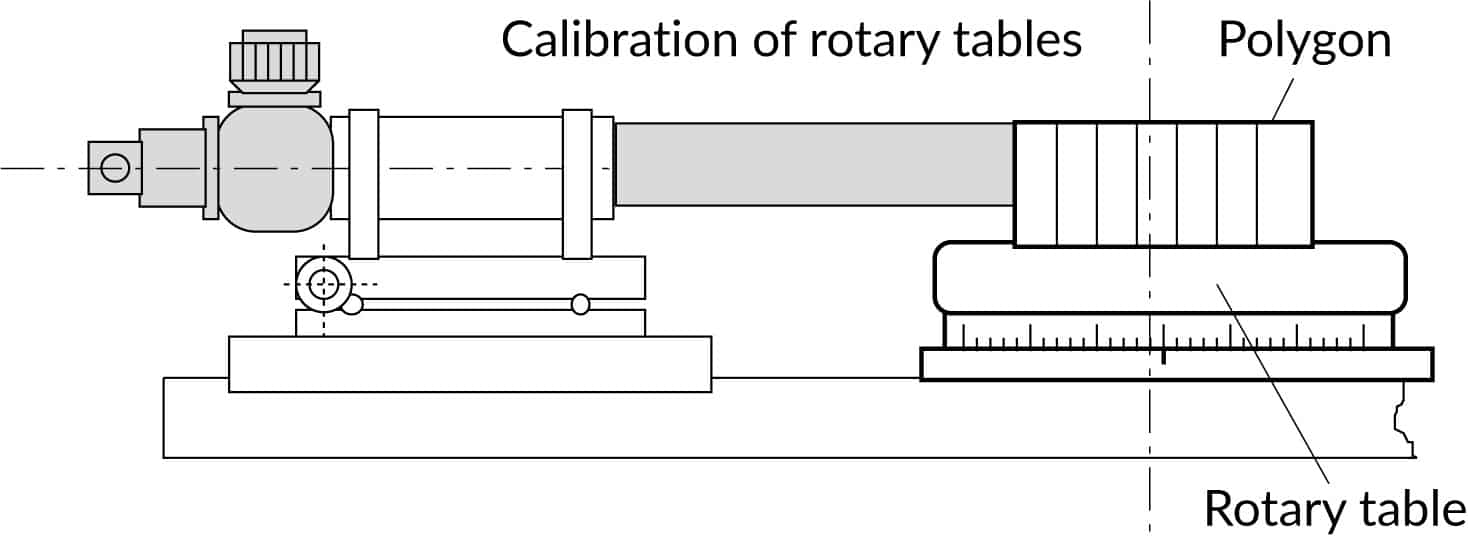
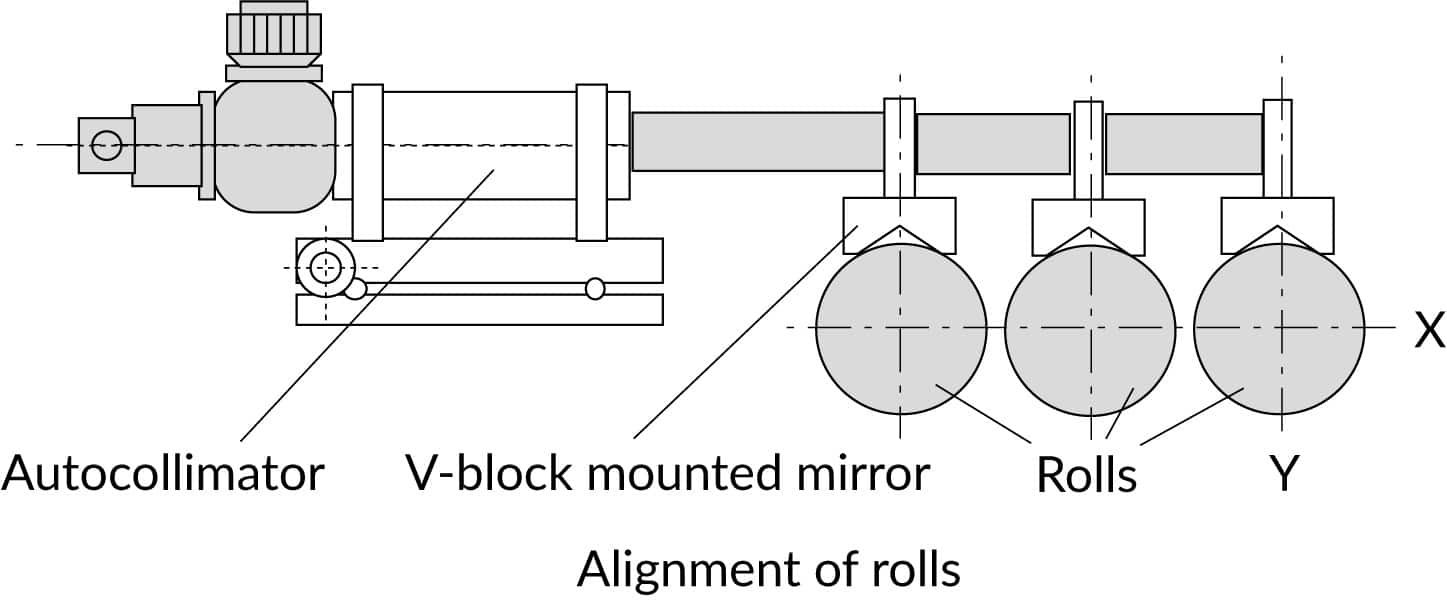
Checking the straightness, squareness, parallelism and flatness
The measurement of geometrical parameters of mechanical parts is a typical application in machine construction, machine tools and aerospace industry.
Measurement of optical and optomechanical parameters
Our products
Our autocollimators are part of the OptiTest® product group. They are available in the following variants:

Focusable Large Field Autocollimator
Large Field Autocollimators with variable focus setting
Possible user specific configurations include
(but are not limited to):
- Focal length and therefore FOV and resolution
- Image/object distance: fixed or user adjustable
- Illumination color: fixed or user adjustable (through filter changer)
- Reticle structure: fixed of user adjustable (through reticle changer)
- Viewing: in-line with or perpendicular to the autocollimator tube axis
Knowledge Base
Autocollimator
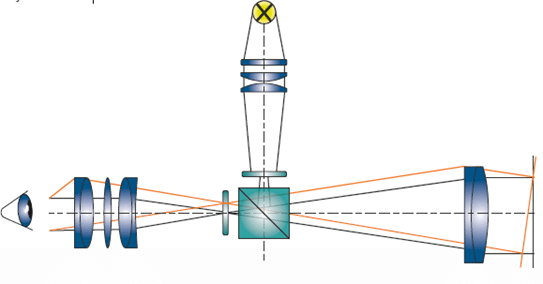
The autocollimator combines both optical tools, the collimator and the telescope into one instrument using a single objective lens. Both beam paths are seperated by using a beamsplitter. The autocollimator is a very sensitive angle measuring device and is thus used for the precise angular adjustment of optical or machine components. Due to the collimated beam (infinity adjustment) the measurement results are independent from the distance to the object under test. The operating principle is explained in the following.

Fig. 1 Schematic cross section of an autocollimator
Fig. 1 shows a schematic cross section of an autocollimator. The collimator components, i.e. light source and collimator reticle, are arranged vertically, while the telescope components, i.e. eyepiece reticle and eyepiece, are arranged horizontally along the mechanical axis of the lens tube. The optical paths are combined via a beam splitter and share the same objective lens.
More knowledge for experts
This article inspired you? Are you looking for further knowledge transfer?
Then you might also be interested in the following topics…
Operating principle
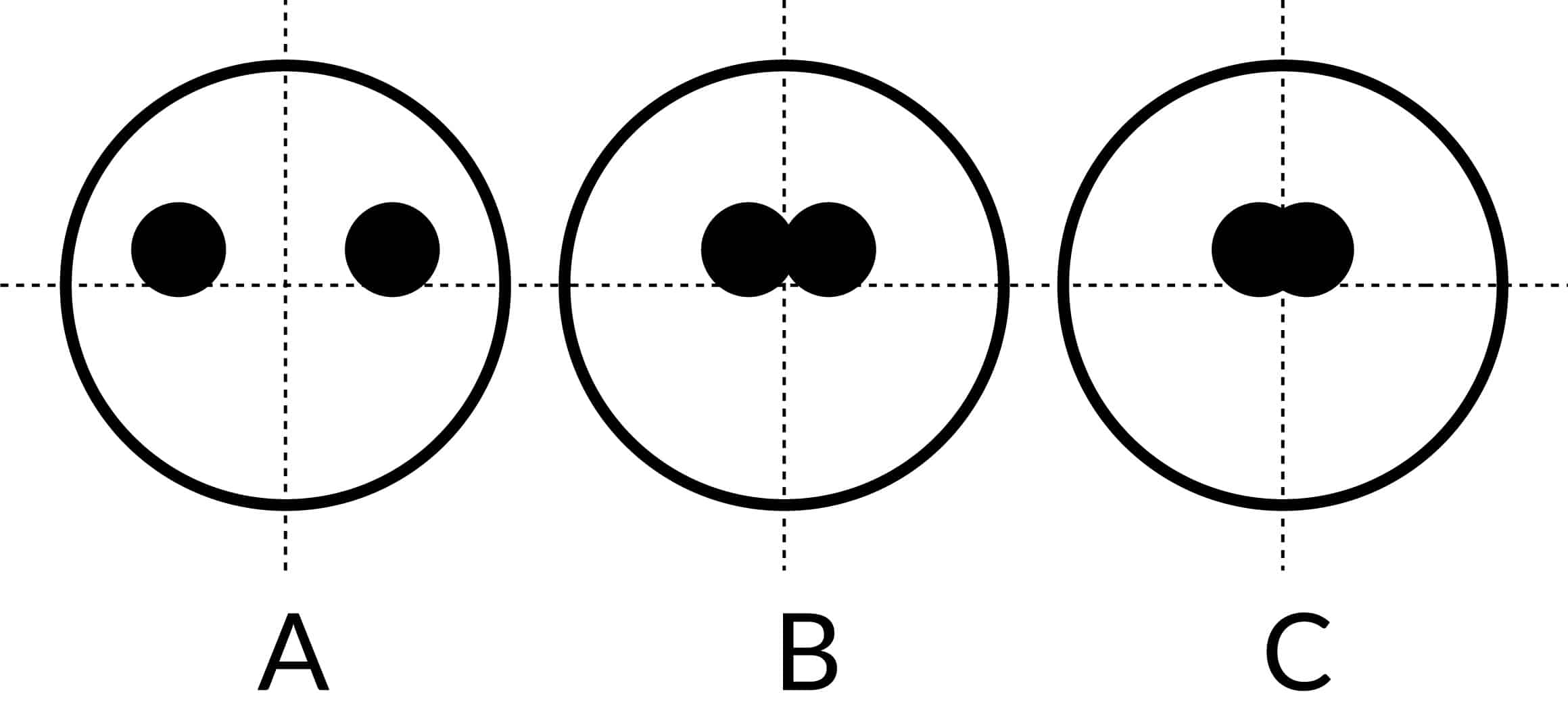
Autocollimation is an optical technique of projecting an illuminated reticle to infinity and receiving the reticle image after reflection on a flat mirror. The reflected image is brought to the focus of the objective lens in which the eyepiece reticle is located. Thus the reflected image of the collimator (illuminated) reticle and the eyepiece reticle can be simultaneously observed. When the collimated beam falls on a mirror which is perpendicular to beam axis, the light is reflected along the same path. Between the reflected image and the eyepiece reticle -which are seen superimposed – no displacement occurs.
If the reflector is tilted by an angle α, the reflected beam is deflected by twice that angle i.e. 2α. The reflected image is now laterally displaced with respect to the eyepiece reticle. The amount of this displacement „d“ is a function of the focal length of the autocollimator and the tilt angle of the reflector: d=2 α f. (α in radians).The tilt angle can be ascertained with the formula:
α = d/(2f)
where f is the effective focal length EFL of the autocollimator. Since the f is a constant of the autocollimator, the eyepiece reticle can be graduated in angle units and the tilt angle can be directly read off.